
Dans un précédent article, je faisais part que dans une logique d'optimisation du ROI, la chose principale sur laquelle nous devrions mettre le focus était l'investissement. En effet, les autres facteurs sont des hypothèses et peuvent être largement en défaveur de ce que l'on escomptait. Des facteurs donc dont nous n'avons pas la maîtrise et sur lesquels il est risqué de se baser, une source souvent de faux espoirs. Un risque qui se réduit par ailleurs en mettant rapidement le produit que l'on crée dans les mains d'utilisateurs pour analyser le comportement réel qu'ils ont avec le produit créé (Cela résout-il le problème posé ? L'achète-t-il ? Cela fait-il émerger d'autres idées ? Etc.)
Il y a quelques jours, une question posée dans la communauté des formateurs pro de ProKanban.org par Prateek Singh, dans le cadre de la création de la nouvelle classe "Accélérer la Valeur d'un Produit", m'a particulièrement intéressé car elle touchait à cet aspect sur lequel j'avais écrit il n'y a pas si longtemps.
La question est la suivante :
Si vous aviez le choix entre
- Scénario 1 : WIP = 1, SLE à 40jours à 85% du temps (SLE ? Mais de quoi il nous parle, consulté mon article sur le sujet ici) et valeur aléatoire entre 1 et 1000. J'ai fixé une borne max pour la complétude d'un élément de potentiel valeur à 81 jours (double du SLE).
- Scénario 2 : WIP = 4, SLE à 10jours à 85% du temps et valeur aléatoire entre 1 et 250. J'ai fixé une borne max pour la complétude d'un élément de potentiel valeur à 31 jours (triple du SLE).
Toute chose étant égale par ailleurs.
Quel serait votre choix pour délivrer un maximum de valeurs ?
Une question à laquelle Prateek a décidé de répondre au travers d'une simulation probabiliste des résultats potentiels.
Sur la base de ce travail initial de Prateek, j'ai ajouté à cette simulation, le paramètre supplémentaire du coût de transaction. En effet après avoir fait quelques simulations qui amenaient à la conclusion que le scénario le plus favorable (et de loin) était le scénario 2 avec des petites hypothèses de valeur (SLE à 10jours à 85% du temps) mais un WIP plus élevé, il était intéressant d'ajouter ce paramètre pour rendre la simulation plus réaliste.
Si vous ne savez pas ce qu'est le coût de transaction, pour faire simple c'est le coût que vous devrez supporter à chaque fois que vous livrerez à vos clients un élément de potentiel valeur. Pour en savoir plus sur cette notion, je vous invite à lire les travaux de Donald G. Reinertsen dans son livre "The principles of product development flow" ou à consulter cette courte vidéo.
Oui, oui vous avez bien lu, le scénario avec un SLE 4 fois moins élevé et donc 4 fois moins de valeur potentiel livrée à chaque fois est celui qui performe le mieux. Ce qui rejoignait mon article précédent où je concluais par "Segmenter son investissement et adopter une stratégie incrémentale, oui, oui et totalement oui !"
Regardons cela de plus prêt.
Pour simuler ces 2 situations, nous avons utilisé la technique de simulation de Monte Carlo (vous ne savez pas ce que c'est ? Je n'ai malheureusement pas encore écrit d'article mais vous pouvez consulter la page wikipédia en attendant). En effet les paramètres de la simulation ont des valeurs incertaines, les possibilités de résultats finaux sont nombreuses et toutes imprédictibles de façon déterministe. La technique de Monte Carlo se prête donc parfaitement bien pour apporter une réponse via une analyse probabiliste des résultats escomptés possibles.
Dans les simulations, à chaque fois qu'un élément de potentiel valeur est livrée, l'équipe reçoit un bonus de 0,1% sur la valeur potentielle du prochain élément, simulant ainsi l'amélioration apportée par l'apprentissage.
Après avoir fait tourner 100 000 fois la simulation sur ces 2 équipes pour une année complète (365 jours), voici les résultats obtenus :
| Centile | Valeur obtenue Scénario 1 | Valeur obtenue Scénario 2 | Facteur de différence entre scénario 2 et 1 |
|---|---|---|---|
| 30% | 5846 | 24940 | 4,3 |
| 50% | 6714 | 25995 | 3,9 |
| 70% | 7628 | 27064 | 3,5 |
| 80% | 8202 | 27717 | 3,4 |
| 90% | 9044,1 | 28632 | 3,2 |
| 95% | 9742 | 29418,05 | 3,0 |
| Min | 1134 | 17837 | 15,7 |
| Max | 16731 | 35158 | 2,1 |
Le "centile" 50% signifie que sur ce scénario 50% des simulations ont amené 6714 unités de valeur ou moins pour le scénario 1 et 25995 ou moins pour le scénario 2.
Soit un facteur de 4,3 fois plus de valeurs apportées pour le scénario 2 par rapport au 1.
Le minimum obtenu avec le scénario 2 est même supérieur au maximum obtenu avec le scénario 1.
Un scénario 2 donc largement gagnant.
Mais qu'en est-il, si on ajoute le facteur du coût de la transaction ? En effet livrée des petits lots (scénario 2) dans ce cas amène un coût de transaction 4x plus fréquent que dans le scénario 1. Cela fait-il pencher la balance en faveur du scénario 1 ? A partir de quel coût de transaction est-ce le cas ? Ce sont des éléments que j'ai ajouté à la simulation initiale de Prateek.
Pour le savoir, c'est reparti pour une simulation de Monte-Carlo, avec d'abord un coût constant de transaction égal à 50 unités de valeur. Ce qui veut dire que pour chaque livraison d'un élément de potentiel valeur, il faudra compter un coût de 50 unités… ce qui parfois rendra négatif le ROI de l'élément, 5% du temps pour le scénario 1, et 20% du temps pour le scénario 2.
| Centile | Valeur obtenue Scénario 1 | Valeur obtenue Scénario 2 | Facteur de différence entre scénario 2 et 1 |
|---|---|---|---|
| 30% | 5226 | 15688 | 3,0 |
| 50% | 6047 | 16508 | 2,7 |
| 70% | 6907 | 17335 | 2,5 |
| 80% | 7450 | 17851 | 2,4 |
| 90% | 8226 | 18576 | 2,3 |
| 95% | 8904 | 19181 | 2,2 |
| Min | 784 | 9537 | 12,2 |
| Max | 14249 | 23987 | 1,7 |
Un scénario 2 toujours largement gagnant, même si un peu moins lié au coût de transaction, mais toujours gagnant de manière très significative.
J'avoue avoir été étonné par ce résultat, je m'attendais à ce que le facteur de différence soit nettement moindre.
Voyons ce qu'il se passe si on bascule à un coût de transaction de 100 unités de valeurs.
Pour rappel cela signifie donc que parfois cela rendra négatif le ROI, 10% du temps pour le scénario 1, et 40% du temps pour le scénario 2.
| Centile | Valeur obtenue Scénario 1 | Valeur obtenue Scénario 2 | Facteur de différence entre scénario 2 et 1 |
|---|---|---|---|
| 30% | 4597 | 6379 | 1,4 |
| 50% | 5359 | 7025 | 1,3 |
| 70% | 6172 | 7682 | 1,2 |
| 80% | 6680 | 8089 | 1,2 |
| 90% | 7405 | 8650 | 1,2 |
| 95% | 8057 | 9120 | 1,1 |
| Min | 438 | 1891 | 4,3 |
| Max | 15966 | 12943 | 0,8 |
Dans ce cas, l'écart se resserre fortement, cependant le scénario 2 est toujours gagnant et malgré que le coût de transaction amène à avoir une livraison sans ROI environ 40% du temps, contrairement à 10% pour l'autre scénario !
Et regardez le minimum obtenu après 100 000 simulations avec ces paramètres, il est 4,3 fois meilleur avec le scénario 2. Ce qui veut dire qu'au pire des cas, cette stratégie vous permettra de minimiser les "pertes".
Essayons un coût de transaction de 120 unités de valeur, et voyons ce que cela donne.
| Centile | Valeur obtenue Scénario 1 | Valeur obtenue Scénario 2 | Facteur de différence entre scénario 2 et 1 |
|---|---|---|---|
| 30% | 4356 | 2639 | 0,6 |
| 50% | 5098 | 3240,5 | 0,6 |
| 70% | 5899 | 3848 | 0,7 |
| 80% | 6399 | 4224 | 0,7 |
| 90% | 7109 | 4732 | 0,7 |
| 95% | 7723 | 5160 | 0,7 |
| Min | 545 | -1417 | -1,4 |
| Max | 12630 | 8560 | 0,7 |
Cette fois le scénario 1 génère le plus de valeurs. Le coût de transaction est cette fois trop élevé pour que la stratégie des petits incréments puissent surpasser une stratégie en plus gros lot.
Un résultat, tout à fait impressionnant. Avant que ces simulations ne soient lancées, j'étais persuadé que le scénario 2 serait gagnant en omettant d'ajouter un coût de transaction à l'équation. Le résultat obtenu était cependant tout à fait surprenant, la différence état énorme (x4).
J'avoue que si j'avais parié sur le coût de transaction qui ferait basculer la balance pour le scénario 1, j'aurai très certainement perdu en misant plutôt autour de 50, que sur plus de 100.
Ces quelques simulations confirment en tout cas pour moi, la conclusion de mon article précédent.
J'insiste donc sur le fait que si vous voulez mettre toutes les chances de votre côté pour délivrer un maximum de valeurs et avoir un bénéfice net optimisé, alors vous avez grand intérêt à réduire la taille de vos lots. Même si cela peut être contre intuitif vis-à-vis du coût de transaction, vous devez pousser à aller à un niveau fin de l'incrément de valeur.
En effet la simulation montre que même si le coût de transaction est égal à 40% de la valeur potentielle maximum escomptée, cela sera tout de même plus intéressant que de délivrer avec une taille de lot 4 fois plus grande (pour ramener la proportion du coût de transaction à 10% de la valeur maximum escomptée).
Vous avez par ailleurs pu noter l'impact sur le bénéfice net qu'entraine une réduction du coût de transaction. Impact d’autant plus important que les incréments de valeur potentiel sont petits.
Si vous ne l'avez pas bien vu voici cela mis en évidence dans le tableau ci-dessous :
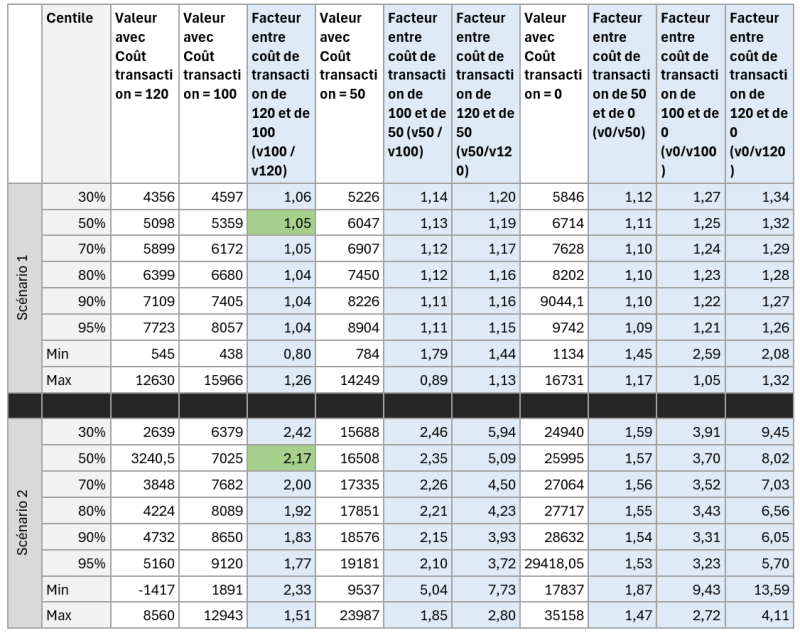
Comparaison toujours faites en prenant en numérateur le coût de transaction le plus faible et au dénominateur le coût de transaction le plus élevé.
Exemple (colorié en vert dans le tableau) entre un coût de transaction de 100 et de 120, le scénario 2 performe à la médiane (centile = 50%) 2,17 fois (ou 117%) plus avec un coût de transaction à 100 qu’à 120.
Alors que sur le scénario 1, ce facteur n’est que de x1,05 (5%).
Envie d'en découvrir plus ? Rejoignez moi dans une de mes formations certifiantes en partenariat avec ProKanban.org.




Ajouter un commentaire
Commentaires